Category:Uniform polyhedra vertex figures
This category lists images of vertex figures for the set of uniform polyhedra. Every uniform polyhedron can be generated by a single vertex figure.
Images are used for two list articles and individual articles for each polyhedron.
Technical details on construction
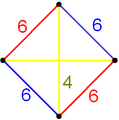
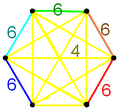
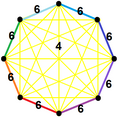
[edit]The vertex figure is a pyramid, defined by a polyhedron vertex at the pyramid apex and the N edge-neighboring vertices a the pyramid base. The base vertices all exist on a plane and on the circumference of a circle.
The lengths of the pyramid base edges are determined by the distance between alternate points on the polygon faces. (Colored faces shown but intersecting faces are not drawn correctly divided.)
The faces on the vertex can be en:regular polygons {p} or regular en:star polygons {p/q}. The sequence of faces can go forwards or backwards around the pyramid.
A general vertex figure can be given as a sequence of n polygons and m is the en:Winding number around the pyramid.
- (p1/q1,p2/q2,p3/q3,...,pn/qn)/m
- Where p/q is a polygon face of p sides and q turns.
- Backwards winding faces are represented by {p/(p-q)}. Example {3/2} is a backwards winding triangle {3/1} and {5/3} is a backwards pentagram {5/2}.
- The winding number m can be zero or greater and is usually only shown if it is two or greater.
Some uniform polyhedra (with two forward and two identical backwards faces) have a winding number of zero and require an explicit base circle radius for it to be contrained to a unique geometry. Example (4.8/3.4/3.8/5) Image:Great_rhombihexahedron_vertfig.png
NOTE: en:Star polygon faces have an ambiguous "interior" definition. They can be drawn in two ways: (1) Filled by an even/odd intersection interior rule, or (2) Calculating new vertices on intersecting edges and filling all interior surfaces of the resulting net. These images are drawn the first way, while polyhedral model builders like Wenninger construct edge (and face) intersections and use the second rule. The underlying geometry is the same - it's just a slightly different visualization.
External links
[edit]- http://home.aanet.com.au/robertw/VertexDesc.html Consistent Vertex Descriptions
- http://web.ukonline.co.uk/polyhedra/uniform/uniform.html Uniform Polyhedra (By Vertex Figures)
- http://www.queenhill.demon.co.uk/polyhedra/filling/filling.htm Filling polytopes
Subcategories
This category has the following 3 subcategories, out of 3 total.
Media in category "Uniform polyhedra vertex figures"
The following 14 files are in this category, out of 14 total.
-
Birectified 16-cell honeycomb verf.png 176 × 176; 5 KB
-
Birectified 16-cell honeycomb verf2.png 174 × 179; 6 KB
-
Birectified 16-cell honeycomb verf3.png 176 × 179; 7 KB
-
Loop pqrs vertex figures.png 777 × 481; 39 KB
-
Omnitruncated 3-simplex honeycomb verf.png 334 × 324; 9 KB
-
Omnitruncated 3-simplex honeycomb verf2.png 323 × 326; 8 KB
-
Omnitruncated 4-simplex honeycomb verf.png 349 × 328; 13 KB
-
Omnitruncated 5-simplex honeycomb verf.png 341 × 330; 16 KB
-
Omnitruncated 6-simplex honeycomb verf.png 814 × 840; 77 KB
-
Omnitruncated 6-simplex verf.png 339 × 315; 15 KB
-
Omnitruncated 7-simplex honeycomb verf.png 517 × 510; 35 KB
-
Snub 24-cell honeycomb verf.png 859 × 854; 33 KB
-
Truncated 24-cell honeycomb B4 verf.png 544 × 591; 19 KB
-
Vertex figures.png 954 × 834; 42 KB