Category:Related sets of 3-bit Walsh permutations; heptagon

 See also category: 15-gon cycles of 4-bit Walsh permutations.

Two inverse permutations in conjugacy classes 7a and 7b

Another pair of inverse permutations
The cycle on the left is the same as in the Heawood graph shown below.

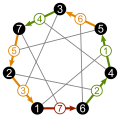
The heptagon cycle in these images is always shown with counter-clockwise arrows (like in the permutation matrix).
The base edge is always the red one, changing all three bits. The yellow arrows change two bits. The green arrows change one.

Heptagon edges are marked with the bitwise XOR of the vertex numbers.
Each edge number is connected to the vertex with the same number.
(When the halves of each arrow are interpreted as edges, this is the Heawood graph.)

There are two chiral variants of the resulting heptagram pattern. It is the same for permutations in the same conjugacy class.
This leads to the following definition of these two conjugacy classes:

Let ${\displaystyle p}$ be the cycle of permutation ${\displaystyle P}$, and let ${\displaystyle n}$ be any integer.
Then ${\displaystyle P}$ is in conjugacy class ${\displaystyle {\begin{cases}{\text{7a}},~~~~{\text{if}}~~~~p{\bigl (}n{\bmod {7}}{\bigr )}~=~p{\bigl (}(n+2){\bmod {7}}{\bigr )}~\oplus ~p{\bigl (}(n+3){\bmod {7}}{\bigr )}\\{\text{7b}},~~~~{\text{if}}~~~~p{\bigl (}n{\bmod {7}}{\bigr )}~=~p{\bigl (}(n-2){\bmod {7}}{\bigr )}~\oplus ~p{\bigl (}(n-3){\bmod {7}}{\bigr )}\end{cases}}}$.

a and b in the following Python code are the cycles of the example permutations.

a = [1, 2, 4, 5, 7, 3, 6]
b = [1, 6, 3, 7, 5, 4, 2]

for n in range(7):
    assert a[n % 7] == a[(n + 2) % 7] ^ a[(n + 3) % 7]
    assert b[n % 7] == b[(n - 2) % 7] ^ b[(n - 3) % 7]