Category:Matching (graph theory)

From Wikimedia Commons, the free media repository

Jump to navigation Jump to search

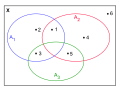
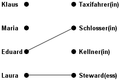
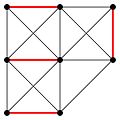
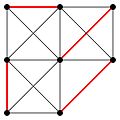
English: In the mathematical discipline of graph theory, a matching or independent edge set in a graph is a set of edges without common vertices. It may also be an entire graph consisting of edges without common vertices.

See also category: Vertex cover problem.

matching

set of edges without common vertices

Upload media

Subclass of

set (edge)

Part of

edge set (subset)

Different from

Authority file
Q1065144 GND ID: 4831446-8 Library of Congress authority ID: sh85082044 J9U ID: 987007555888405171
Reasonator Scholia Wikidocumentaries PetScan statistics WikiMap Locator tool KML file Search depicted

Subcategories

This category has only the following subcategory.

T

Triple-Graph-Grammar (7 F)

Media in category "Matching (graph theory)"

The following 58 files are in this category, out of 58 total.

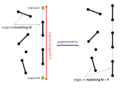
Augmenting path.png 812 × 593; 14 KB
Beispiel Ungarische Methode.svg 512 × 461; 16 KB
Bip2maxflow.jpg 3,891 × 2,500; 456 KB
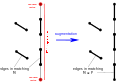
Blossom contraction.png 836 × 578; 36 KB
Blossom Counter.svg 346 × 298; 4 KB
Blossom end point path lifting.png 875 × 484; 26 KB
Blossoms can't be ignored.svg 274 × 297; 5 KB
Chord diagrams K6 matchings.svg 972 × 576; 26 KB
Cross blossom path lifting.png 941 × 410; 32 KB
Dilworth-via-König.svg 800 × 494; 21 KB
Edmonds augmenting path (vi).svg 800 × 550; 47 KB
Edmonds augmenting path.svg 800 × 550; 47 KB
Edmonds blossom (vi).svg 700 × 550; 81 KB
Edmonds blossom.svg 700 × 550; 81 KB
Edmonds lifting end point.svg 750 × 850; 122 KB
Edmonds lifting path (vi).svg 800 × 860; 153 KB
Edmonds lifting path.svg 800 × 860; 153 KB
Edmonds-example-1.svg 325 × 408; 11 KB
Edmonds-example-2.svg 417 × 446; 14 KB
Edmonds-example-3.svg 240 × 369; 7 KB
Edmonds-example-t7.svg 100 × 288; 5 KB
Forest expansion.png 800 × 583; 31 KB
Halls theorem matching graph theory.svg 401 × 416; 17 KB
Halls theorem matching graph theory2.svg 401 × 416; 20 KB
Halls theorem negartive example.svg 681 × 409; 20 KB
Halls theorem negartive example2.svg 605 × 406; 20 KB
Halls theorem positive example.svg 692 × 461; 27 KB
Halls theorem positive example2.svg 534 × 407; 21 KB
HeiratssatzGraphentheorie.PNG 182 × 195; 4 KB
HeiratssatzNegativBeispiel.PNG 345 × 209; 6 KB
HeiratssatzPositivBeispiel.PNG 426 × 298; 9 KB
K4 matchings.svg 270 × 351; 9 KB
Koenigs-theorem-graph.png 450 × 306; 15 KB
Koenigs-theorem-graph.svg 450 × 306; 2 KB
Koenigs-theorem-proof.svg 333 × 423; 5 KB
Koenigs-theorem-proof2.svg 325 × 359; 9 KB
Matching (graph theory).jpg 452 × 452; 55 KB
Maximal matching.jpg 452 × 452; 54 KB
Maximal-matching.svg 300 × 60; 18 KB
Maximal-simple.svg 80 × 130; 491 bytes
Maximum matching.jpg 452 × 452; 58 KB
Maximum-matching-labels.svg 300 × 60; 20 KB
Maximum-matching.svg 300 × 60; 19 KB
Methode Habr.JPG 254 × 293; 31 KB
Minimum cut in a bipartite graph.svg 2,488 × 1,463; 43 KB
Minimum-edge-cover-from-maximum-matching.svg 200 × 60; 15 KB
Path detection.png 837 × 580; 38 KB
Path lifting.png 859 × 584; 37 KB
Perfect matching 1.jpg 452 × 452; 49 KB
Perfect matching 2.jpg 452 × 452; 52 KB
Perfect matching qtl1.svg 510 × 300; 101 KB
Perfect-simple.svg 80 × 130; 562 bytes
SecretaryProblemHeuristicPlot.png 1,201 × 901; 51 KB
Stakan.svg 143 × 62; 7 KB
Sumner claw-free matching.svg 315 × 198; 2 KB
Sylvester counter.svg 200 × 200; 686 bytes
Ungmeth1.JPG 333 × 517; 32 KB
Vertex-cover-from-maximal-matching.svg 200 × 60; 14 KB

Retrieved from "https://commons.wikimedia.org/w/index.php?title=Category:Matching_(graph_theory)&oldid=332556384"

Non-topical/index: