Category:Haar wavelet

**Haar wavelet**
	the first wavelet
	Upload media
	Wikipedia
Instance of	mathematical concept;
Subclass of	Daubechies wavelet;
Named after	Alfréd Haar;
Authority file
	Q766198;
	Reasonator; Scholia; Wikidocumentaries; PetScan; statistics; WikiMap; Locator tool; KML file; Search depicted;

Čeština: Haarova vlnka je nejstarší a nejjednodušší vlnka. V roce 1909 ji zkonstruoval maďarský matematik Alfréd Haar, který tak objevil alternativní ortonormální systém k Fourierovým bázím.

Deutsch: Das Haar-Wavelet ist das erste in der Literatur bekannt gewordene Wavelet und wurde 1909 von Alfréd Haar vorgeschlagen. Es ist außerdem das einfachste bekannte Wavelet und kann aus der Kombination zweier Rechteckfunktionen gebildet werden.

English: In mathematics, the Haar wavelet is a sequence of rescaled "square-shaped" functions which together form a wavelet family or basis. Wavelet analysis is similar to Fourier analysis in that it allows a target function over an interval to be represented in terms of an orthonormal function basis. The Haar sequence is now recognised as the first known wavelet basis and extensively used as a teaching example.

Español: En matemáticas, el wavelet de Haar es una cierta secuencia de funciones. Ahora se le reconoce como el primer wavelet conocido. Esta secuencia fue propuesta en 1909 por Alfred Haar. Haar usó estas funciones para dar un ejemplo de un sistema ortonormal contable para el espacio de las funciones de cuadrado integrable en la recta real. El estudio de los wavelets, e incluso el termino "wavelet", no vinieron hasta mucho después. Como un caso especial de wavelet de Daubechies, también es llamado D2.

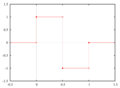
فارسی: موجک هار سری خاصی از توابع است که اکنون به عنوان اولین موجک شناخته می‌شود. این سری اولین بار توسط آلفرد هار، ریاضیدان مجاری در سال ۱۹۰۹ پیشنهاد شد. موجک هار ساده‌ترین موجک ممکن می‌باشد. مشکل این موجک این است که پیوسته نیست و در نتیجه مشتق‌پذیر نمی‌باشد. موجک مادر هار به شکل زیر تعریف می‌شود:

Français : L'ondelette de Haar, ou fonction de Rademacher, est une ondelette créée par Alfréd Haar en 1909. On considère que c'est la première ondelette connue. Elle est la plus simple à comprendre et à implémenter. C'est une fonction dilatée et/ou translatée de la fonction mère ψ qui vaut :

Italiano: La wavelet Haar è stata la prima wavelet ad essere proposta nel 1909 da Alfréd Haar

Lietuvių: Haaro vilnelė arba Haaro funkcija - matematinė funkcija, pirmą kartą pasiūlyta Alfredo Haaro 1909 m. Ji laikoma istoriškai pirmąja vilnele.

Polski: Falka Haara jest pierwszą znaną falką, została wprowadzona przez Alfréda Haara w 1909 lub 1910 r. Jest to szczególnie prosta falka, jej funkcja-matka określona jest wzorem:

Português: A Transformada de Haar é um transformada matemática discreta usada no processamento e análise de sinais, na compressão de dados e em outras aplicações de engenharia e ciência da computação. Ela foi proposta em 1909 pelo matemático húngaro Alfred Haar. A transformada de Haar é um caso particular de transformada discreta de wavelet, onde o wavelet é um pulso quadrado definido por:

Русский: Вейвлет Хаа́ра — один из первых и наиболее простых вейвлетов. Он был предложен венгерским математиком Альфредом Хааром в 1909 году. Вейвлеты Хаара ортогональны, обладают компактным носителем, хорошо локализованы в пространстве, но не являются гладкими. Впоследствии Ингрид Добеши стала развивать теорию ортогональных вейвлетов и предложила использовать функции, вычисляемые итерационным путем, названные вейвлетами Добеши.

Svenska: höger|miniatyr|Haars wavelet.

中文：哈爾小波轉換是於1909年由Alfréd Haar所提出，是小波轉換(Wavelet transform)中最簡單的一種轉換，也是最早提出的小波轉換。他是多贝西小波的於N=2的特例，可稱之為D2