File:XCubed Fourier Series Approximation n=7,15.svg

From Wikimedia Commons, the free media repository
Jump to navigation Jump to search

Original file (SVG file, nominally 720 × 460 pixels, file size: 83 KB)

Captions

Captions

Add a one-line explanation of what this file represents
Description

This is a graph of x3, periodic on (-π,π), with the Fourier Series Approximations drawn in at k=7 (red) and k=15 (blue). The approximation is given by

.

This is the counterpart to this, which has just the original function drawn in.
Date
Source Own Drawing, Plotted in Mathematica, edited in Inkscape.
Author Inductiveload
Permission
(Reusing this file)
Public domain I, the copyright holder of this work, release this work into the public domain. This applies worldwide.
In some countries this may not be legally possible; if so:
I grant anyone the right to use this work for any purpose, without any conditions, unless such conditions are required by law.
Other versions image:XCubed Periodic (-pi, pi).svg

Mathematica Code

[edit]
f[x_] = x^3;

ffour[x_, k_] =
  Hold[
   Sum[
    ((-2*(-1)^n*(Pi^2*n^2 - 6))/(n^3))*Sin[n*x],
    {n, 1, k}]
   ];

Plot[
 {f[Mod[x, 2 \[Pi], -\[Pi]]],
  ReleaseHold[ffour[x, 7]],
  ReleaseHold[ffour[x, 15]]},
 {x, -2 Pi, 2 Pi}]

File history

Click on a date/time to view the file as it appeared at that time.

Date/TimeThumbnailDimensionsUserComment
current02:29, 23 February 2008Thumbnail for version as of 02:29, 23 February 2008720 × 460 (83 KB)Inductiveload (talk | contribs){{Information |Description= |Source= |Date= |Author= |Permission= |other_versions= }}
02:00, 23 February 2008Thumbnail for version as of 02:00, 23 February 2008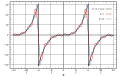720 × 460 (83 KB)Inductiveload (talk | contribs){{Information |Description= |Source= |Date= |Author= |Permission= |other_versions= }}
01:21, 10 February 2007Thumbnail for version as of 01:21, 10 February 2007625 × 386 (189 KB)Inductiveload (talk | contribs){{Information |Description=This is a graph of x<sup>3</sup>, periodic on (-π,π), with the Fourier Series Approximations drawn in at k=7 (red) and k=15 (blue). The approximation is given by <math>f\left( x \right) = \sum\limits_{n = 1}^k {{{ - 2\lef

You cannot overwrite this file.

The following 2 pages use this file:

File usage on other wikis

The following other wikis use this file:

Retrieved from "https://commons.wikimedia.org/w/index.php?title=File:XCubed_Fourier_Series_Approximation_n%3D7,15.svg&oldid=452053220"